The Method of Moderation: Illustrative Notebook

# Import Econ-ARK styling and display header
from style import (
    HEADER_HTML_NOTEBOOK,
    apply_ark_style,
    apply_notebook_css,
)

# Apply Econ-ARK branding and styling
apply_ark_style()
apply_notebook_css()



# Display Econ-ARK header (for Jupyter notebooks)
from IPython.display import HTML, display

display(HTML(HEADER_HTML_NOTEBOOK))

Author: Alan Lujan, Johns Hopkins University

This notebook provides a pedagogical introduction to the Method of Moderation (MoM), a novel technique for solving consumption-saving models with superior accuracy and stability. We begin by motivating the problem that MoM solves—the “extrapolation problem” inherent in sparse-grid implementations of the Endogenous Grid Method (EGM). We then build the theoretical foundations for MoM, demonstrating how it leverages analytical bounds to ensure economically sensible behavior across the entire state space.

Model Foundations: The Friedman-Muth Income Process¶

To understand the consumption-saving problem, we must first define the economic environment. We adopt the canonical framework of an agent who receives a stream of labor income that is subject to both permanent and transitory shocks. This income process, first conceptualized by Friedman (1957) and later formalized stochastically by Muth (1960), provides a realistic foundation for modeling household financial behavior. It captures two key features of real-world income dynamics:

Permanent Shocks: Unexpected changes to lifetime earning potential (e.g., a promotion or a permanent disability).
Transitory Shocks: Temporary fluctuations in income (e.g., a one-time bonus or a temporary layoff).

The model used in this notebook, drawn from Carroll (2020), implements this income process and provides the basis for solving the consumer’s optimization problem.

The Extrapolation Problem in Consumption-Saving Models¶

At its core, the Method of Moderation (MoM) is designed to solve a persistent challenge in computational economics: the extrapolation problem. This issue is particularly pronounced in sparse-grid implementations of the Endogenous Grid Method (EGM), a widely-used technique for solving dynamic stochastic optimization problems.

When EGM is used to solve a consumption-saving model, it computes the optimal consumption policy at a finite set of grid points. However, to simulate agent behavior or analyze policy implications, we often need to evaluate the consumption function at points that lie outside this pre-computed grid. Standard practice is to extrapolate from the grid, but this can lead to results that violate fundamental economic theory. Specifically, linear extrapolation can predict negative precautionary saving, which implies that consumers with greater income uncertainty would save less than those with no uncertainty—a direct contradiction of established economic principles Leland, 1968Sandmo, 1970Kimball, 1990.

MoM addresses this problem by abandoning direct extrapolation of the consumption function. Instead, it operates in a transformed space defined by two analytical, theoretically-grounded bounds. This approach builds on a long literature on “buffer-stock” saving behavior Carroll, 1997, which has established theoretical properties of consumption functions under uncertainty Stachurski & Toda, 2019Ma et al., 2020. The two bounds are:

The Optimist’s Solution: A consumer who ignores all future income risk.
The Pessimist’s Solution: A consumer who assumes the worst possible income realization in all future periods.

The true, “realist” consumption function must lie between these two extremes. MoM respects this by interpolating a moderation ratio that is guaranteed to remain within these bounds. The result is a consumption function that is not only computationally efficient but also economically coherent across the entire state space.

Key Insight: By transforming the problem into a space defined by theoretical bounds, MoM ensures that its solutions are always economically sensible, even far outside the computed grid. This notebook will walk through the practical implementation of this insight, from demonstrating the EGM’s extrapolation failure to building the MoM solution step-by-step.

from __future__ import annotations

import numpy as np
from moderation import (
    IndShockEGMConsumerType,
    IndShockMoMConsumerType,
)
from plotting import (
    plot_consumption_bounds,
    plot_logit_function,
    plot_moderation_ratio,
    plot_mom_mpc,
    plot_precautionary_gaps,
    plot_value_functions,
)

# Model setup: Consumer with income uncertainty
params = {
    "CRRA": 2.0,
    "DiscFac": 0.96,
    "Rfree": [1.02],
    "TranShkStd": [1.0],
    "cycles": 1,
    "LivPrb": [1.0],
    "vFuncBool": True,
    "CubicBool": True,
    "PermGroFac": [1.0],
    "PermShkStd": [0.0],
    "TranShkCount": 7,
    "UnempPrb": 0.0,
    "BoroCnstArt": None,
}

# Dense grid for "truth" solution (high precision)
dense_grid = {"aXtraMin": 0.001, "aXtraMax": 40, "aXtraCount": 500, "aXtraNestFac": 3}

# Sparse grid for practical comparison (5 points only)
sparse_grid = {"aXtraMin": 0.001, "aXtraMax": 4, "aXtraCount": 5, "aXtraNestFac": -1}

# Solve three versions: Truth (dense EGM), Sparse EGM, Sparse MoM
IndShockTruth = IndShockEGMConsumerType(**(params | dense_grid))
IndShockTruth.solve()
IndShockTruthSol = IndShockTruth.solution[0]

# Unpack theoretical bounds (same for all methods)
TruthOpt = IndShockTruthSol.Optimist
TruthPes = IndShockTruthSol.Pessimist
TruthTight = IndShockTruthSol.TighterUpperBound

# Sparse EGM solution (standard approach)
IndShockEGMApprox = IndShockEGMConsumerType(**(params | sparse_grid))
IndShockEGMApprox.solve()
IndShockEGMApproxSol = IndShockEGMApprox.solution[0]

# Sparse MoM solution (same grid, different method)
IndShockMoMApprox = IndShockMoMConsumerType(**(params | sparse_grid))
IndShockMoMApprox.solve()
IndShockMoMApproxSol = IndShockMoMApprox.solution[0]

# Grid parameters for plotting
mNrmMax = IndShockMoMApproxSol.mNrmMin + IndShockMoMApprox.aXtraGrid.max()

Consumption Function Analysis¶

The first set of figures will focus on the core of the consumption-saving problem: the consumption function, $c(m)$ , which maps market resources, $m$ , to a chosen level of consumption. We will demonstrate the extrapolation problem inherent in the standard EGM and show how the Method of Moderation resolves it by respecting theoretical bounds.

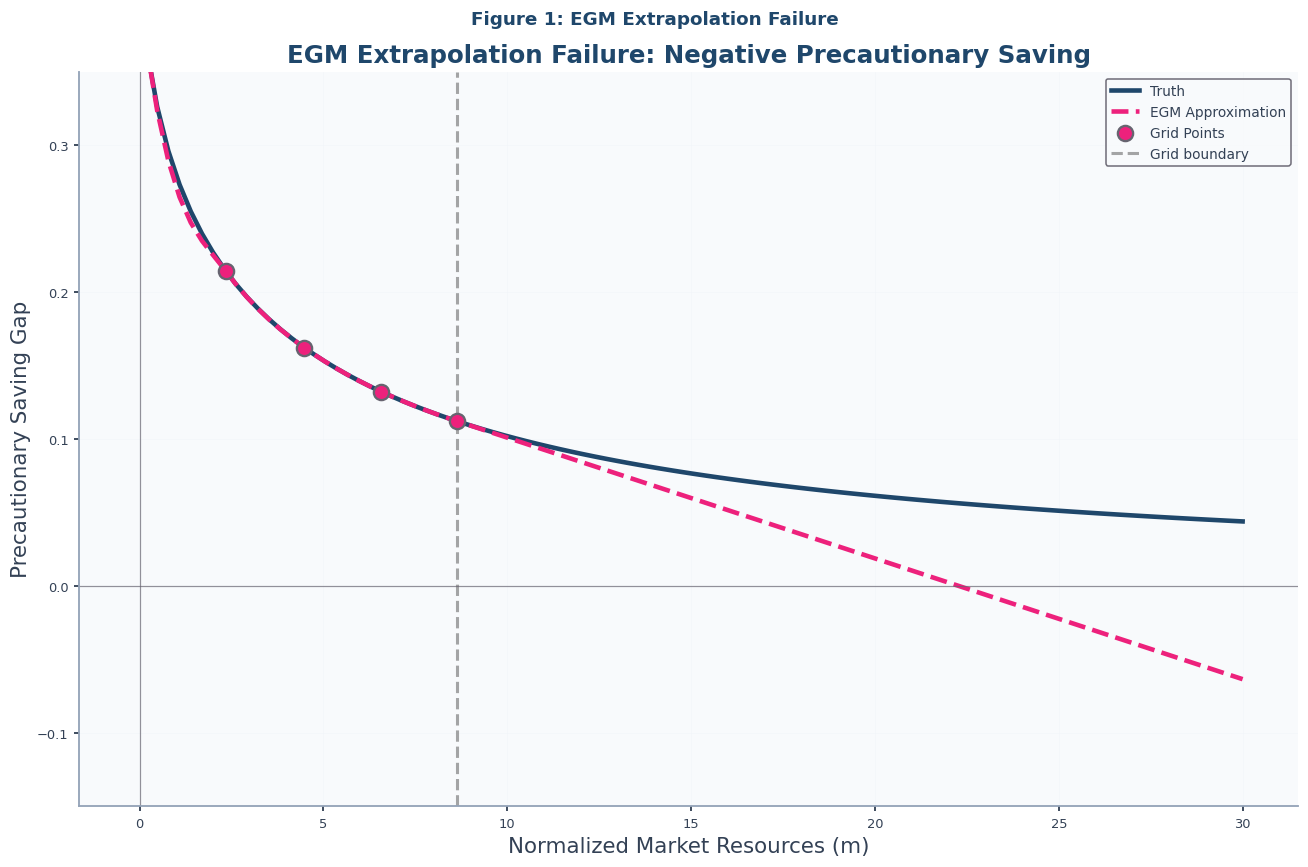
Figure 1: The EGM Extrapolation Problem¶

At the heart of any numerical solution to a consumption-saving problem lies the challenge of extrapolation. Because we can only compute the solution at a finite number of points, we must have a reliable way to evaluate the policy function at points outside this grid. Economic theory provides a powerful test of any method’s extrapolation properties: the precautionary saving gap.

This gap, defined as the difference between the consumption of a perfect-foresight “optimist” and that of a “realist” facing uncertainty, should always be positive. The presence of uninsurable income risk should lead consumers to save more (and thus consume less) than they would in a certain world. However, as demonstrated in the paper and illustrated in Notebook-code (which corresponds to Figure 1 in the academic paper), standard EGM struggles with this constraint when extrapolating Carroll, 2006.

# Define the precautionary saving gap functions
def truth_gap(m):
    """True precautionary saving gap."""
    return TruthOpt.cFunc(m) - IndShockTruthSol.cFunc(m)


def egm_approx_gap(m):
    """EGM approximation gap."""
    return TruthOpt.cFunc(m) - IndShockEGMApproxSol.cFunc(m)


# Test extrapolation over a wide range including high wealth levels
# Extend from near borrowing constraint to high wealth to capture all grid points
m_grid_wide = np.linspace(IndShockEGMApproxSol.mNrmMin + 0.001, 30, 100)

# Figure 1: EGM Extrapolation Failure
# Grid points will be handled internally by plotting functions

plot_precautionary_gaps(
    m_grid=m_grid_wide,
    truth_gap=truth_gap(m_grid_wide),
    approx_gap=egm_approx_gap(m_grid_wide),
    legend="EGM Approximation",
    title="Figure 1: EGM Extrapolation Failure",
    subtitle="EGM Extrapolation Failure: Negative Precautionary Saving",
    solution=IndShockEGMApproxSol,
    grid_points=True,
)

EGM in the Literature

The Endogenous Grid Method (Carroll (2006)) is a powerful and widely-used tool in computational economics. Its applications have been extended to solve multi-dimensional problems Barillas & Fernández-Villaverde, 2007, models with occasionally binding constraints Hintermaier & Koeniger, 2010, non-smooth and non-concave problems Fella, 2014, and discrete-continuous choice models Iskhakov et al., 2017. For a comprehensive treatment of the theory and practice of EGM, see White, 2015.

A critical step in implementing any numerical solution is the discretization of continuous stochastic processes. Standard methods for discretizing income shocks include those proposed by Tauchen & Hussey, 1991 and Tauchen, 1986.

Figure 2: Truth Bounded by Theory¶

Having established the extrapolation problem, we now turn to the theoretical foundation of its solution. The Method of Moderation is built upon a crucial insight from consumption theory: the optimal consumption function for a “realist” consumer facing uncertainty is always bounded by the consumption functions of two hypothetical consumers for whom the problem has a simple, analytical solution. These are the “optimist” and the “pessimist.”

This figure illustrates these theoretical bounds, demonstrating that the true, high-precision consumption function (our “Truth” solution) lies neatly between them. This provides the theoretical justification for the MoM’s approach, as shown in Notebook-code (which corresponds to Figure 2 in the academic paper).

# Create wealth grid for evaluation and plotting (matches paper ranges)
m_grid = np.linspace(IndShockTruthSol.mNrmMin + 0.01, 10, 100)

# Evaluate consumption functions on the grid
c_truth = IndShockTruthSol.cFunc(m_grid)  # True optimal consumption
c_opt = TruthOpt.cFunc(m_grid)  # Optimist consumption
c_pes = TruthPes.cFunc(m_grid)  # Pessimist consumption

# Figure 2: Truth Bounded by Theory
plot_consumption_bounds(
    m_grid=m_grid,
    c_main=c_truth,
    c_opt=c_opt,
    c_pes=c_pes,
    title="Figure 2: Truth Bounded by Economic Theory",
    subtitle="True Consumption Always Lies Between Theoretical Bounds",
    legend="Truth",
    grid_points=False,  # No grid points for theoretical bounds
)

Key Theoretical Insight

The realist consumption function $\cFuncReal(\mNrm)$ lies between the optimist $\cFuncOpt(\mNrm)$ and pessimist $\cFuncPes(\mNrm)$ bounds, reflecting precautionary saving motives. This theoretical constraint, $\cFuncPes(\mNrm) \leq \cFuncReal(\mNrm) \leq \cFuncOpt(\mNrm)$ , is the foundation for the Method of Moderation Carroll & Shanker, 2024. The existence of a lower bound on consumption (and thus an upper bound on borrowing) is a key result from the literature on general equilibrium models with incomplete markets Aiyagari, 1994Huggett, 1993. This “natural borrowing constraint” arises because consumers must be able to repay their debts, which is not possible if their income can fall to a low level with positive probability. Consequently, the consumption function is not well-defined for levels of market resources below this lower bound Zeldes, 1989Deaton, 1991.

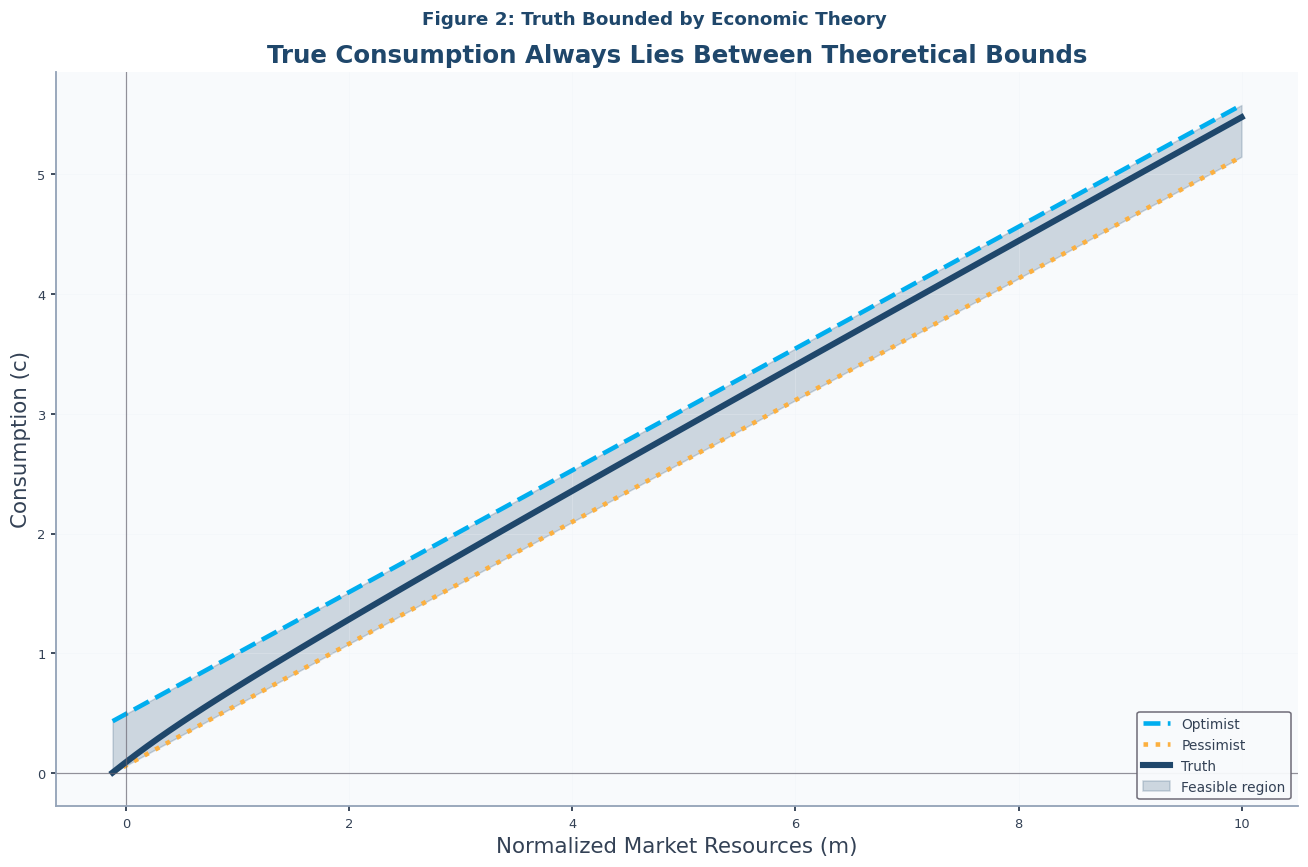
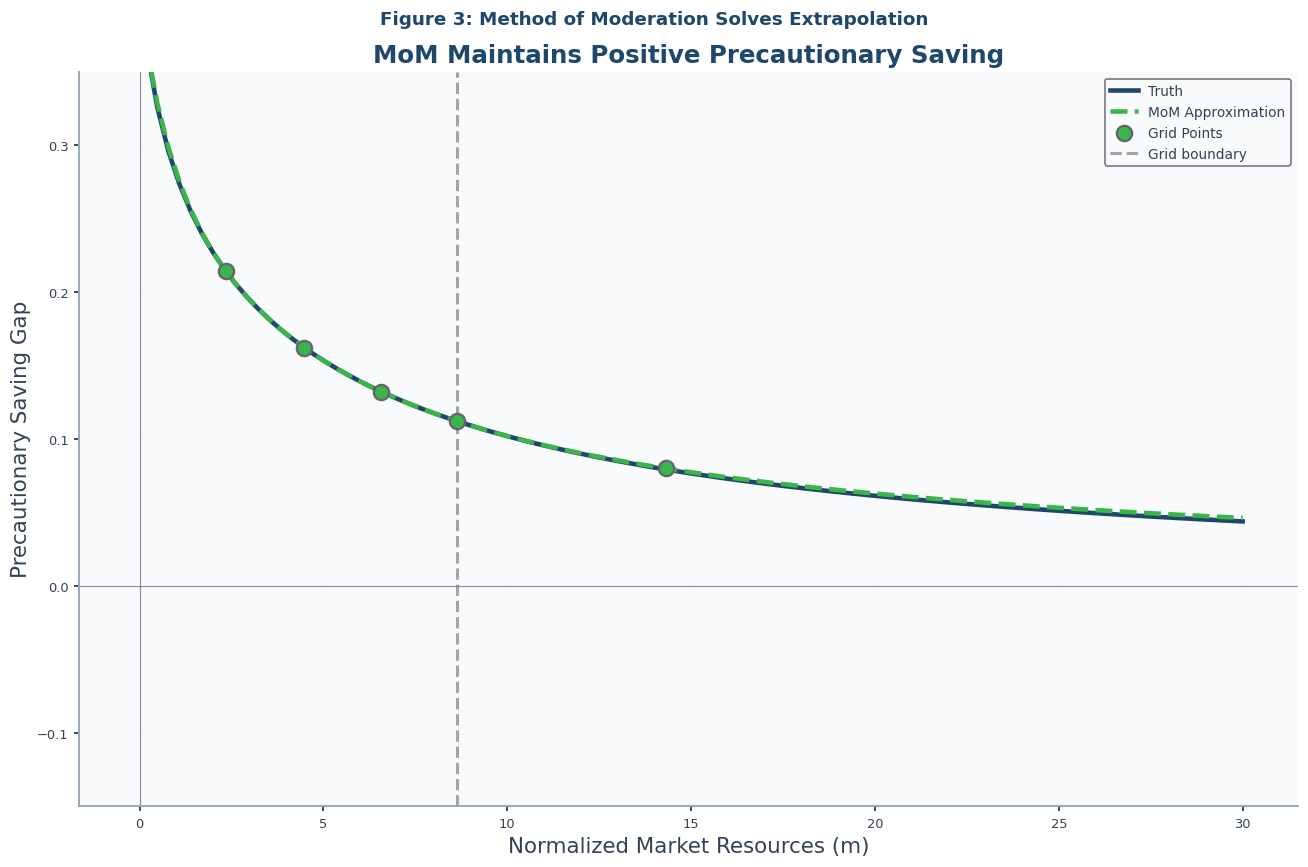
Figure 3: Method of Moderation Solution¶

With the theoretical bounds established, we can now demonstrate how the Method of Moderation uses them to solve the extrapolation problem. Instead of directly interpolating the consumption function, MoM interpolates a moderation ratio that measures where the realist’s consumption lies relative to the optimist and pessimist bounds.

Because this ratio is interpolated in a transformed space that guarantees it will respect the bounds, the resulting consumption function also respects them. As this figure shows, the MoM approximation of the precautionary saving gap remains positive and closely tracks the true solution, even far beyond the computed grid. The success of this approach is clearly demonstrated in Notebook-code (which corresponds to Figure 3 in the academic paper).

# Define MoM gap function
def mom_approx_gap(m):
    """MoM approximation gap."""
    return TruthOpt.cFunc(m) - IndShockMoMApproxSol.cFunc(m)


# Figure 3: Method of Moderation Success
# Grid points will be handled internally by plotting functions

plot_precautionary_gaps(
    m_grid=m_grid_wide,
    truth_gap=truth_gap(m_grid_wide),
    approx_gap=mom_approx_gap(m_grid_wide),
    legend="MoM Approximation",
    title="Figure 3: Method of Moderation Solves Extrapolation",
    subtitle="MoM Maintains Positive Precautionary Saving",
    solution=IndShockMoMApproxSol,
    grid_points=True,
)

# Optional: Example of plotting multiple methods on same figure
# plot_precautionary_gaps(
#     m_grid=m_grid_wide,
#     truth_gap=truth_gap(m_grid_wide),
#     approx_gap=[egm_approx_gap(m_grid_wide), mom_approx_gap(m_grid_wide)],
#     legend=["EGM Approximation", "MoM Approximation"],
#     title="Figure 3: Method Comparison",
#     subtitle="EGM vs MoM Extrapolation Performance",
#     solution=IndShockMoMApproxSol,  # Can use either solution for grid points
#     grid_points=True,
# )

The Method of Moderation builds on EGM’s computational strengths while addressing the extrapolation challenge through economic theory. Following the paper’s algorithm, the key insight is that optimal consumption is always bounded between the optimist and pessimist consumption functions, both of which have known analytical solutions.

MoM Algorithm Details

Instead of extrapolating consumption directly (which can violate bounds), MoM follows these steps (notation matches the paper):

Solve standard EGM to get realist consumption at gridpoints
Transform to log excess resources $\logmNrmEx = \log(\mNrm - \mNrmMin)$ for convenient interpolation domain
Compute moderation ratio $\modRte(\logmNrmEx) = \dfrac{\cFuncOpt - \cFuncReal}{\hNrmEx\,\MPCmin} = \dfrac{\cFuncOpt - \cFuncReal}{\cFuncOpt - \cFuncPes} \in [0,1]$ (paper Eq. (12))
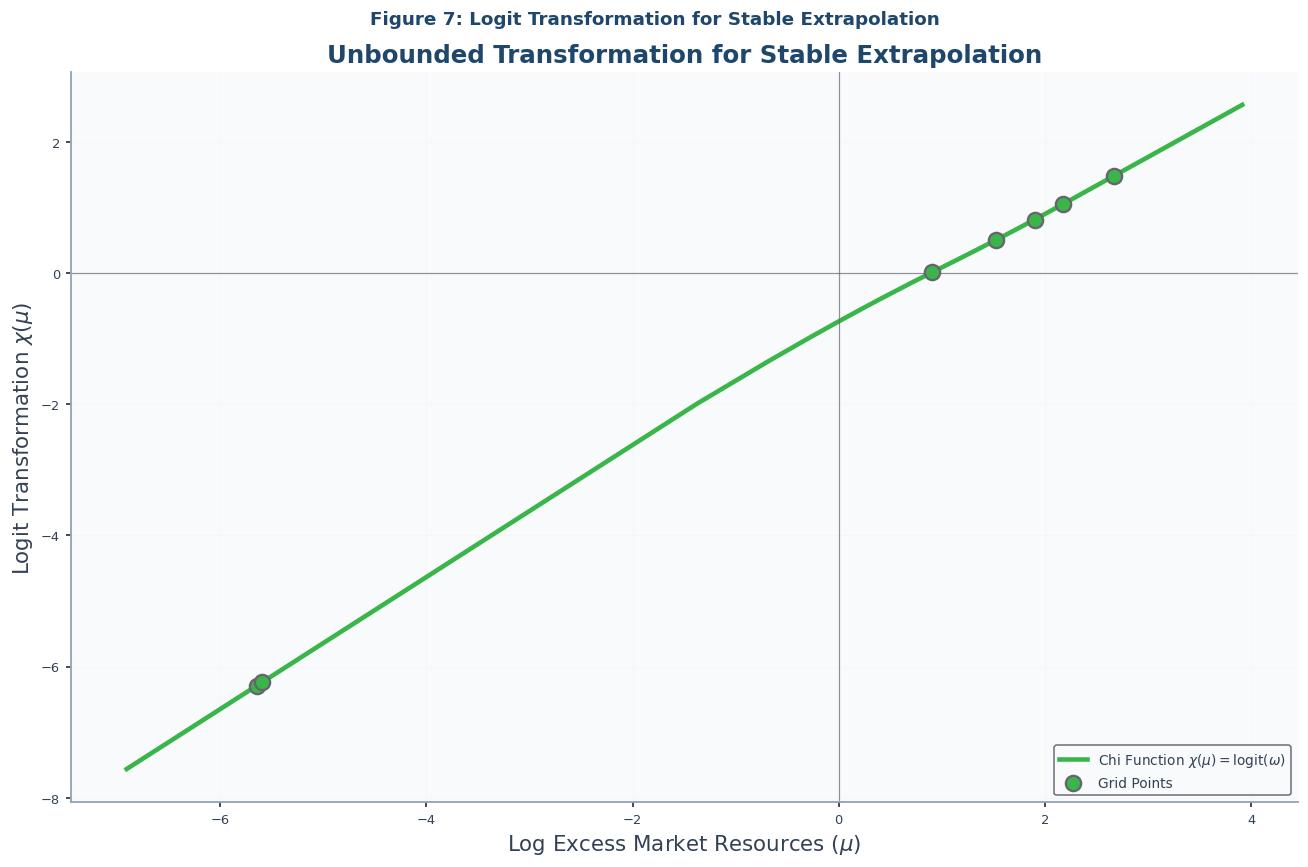
Apply transformation $\logitModRte(\logmNrmEx) = \log((1-\modRte)/\modRte)$ for asymptotic linearity
Interpolate $\logitModRte(\logmNrmEx)$ function with derivatives for smooth extrapolation
Reconstruct consumption using $\cFuncReal = \cFuncOpt - \modRte \cdot (\cFuncOpt - \cFuncPes)$

This approach ensures consumption always stays within economic bounds while achieving excellent extrapolation properties through the asymptotically linear transformation function, as derived in the paper.

The quality of this method relies on accurate function approximation between gridpoints Santos, 2000, and the bracketing approach complements work on bounding numerical errors in dynamic models Judd et al., 2017. While linear interpolation is simple, cubic Hermite interpolation Fritsch & Carlson, 1980Fritsch & Butland, 1984Hyman, 1983 offers superior accuracy by matching not only the function’s level but also its derivative at each gridpoint. This ensures that the numerical solution satisfies the Euler equation at the gridpoints themselves Benveniste & Scheinkman, 1979Milgrom & Segal, 2002. For even better shape-preservation, monotone cubic Hermite schemes can be employed Boor, 2001. The similarity of MPCs under certain conditions Chipeniuk et al., 2021 helps explain why simpler linear bounds often perform well. The HARK toolkit implements cubic Hermite interpolation for this reason.

Figure 4: MoM Consumption Function¶

Having shown that MoM produces a precautionary saving gap with the correct theoretical properties, we can now examine the consumption function itself. This figure plots the MoM consumption function against the same theoretical bounds we saw in Figure 2.

As expected, the MoM solution remains strictly between the optimist and pessimist bounds. The figure also introduces a tighter upper bound. This bound is derived from the maximum possible marginal propensity to consume ( $\MPCmax$ ) as market resources approach the natural borrowing constraint. The existence of such a bound is a key result from the buffer-stock saving literature Carroll, 2001, with explicit formulas for the limiting MPC derived in Ma & Toda, 2021 and Carroll & Toche, 2009. The fact that the MoM solution respects this tighter bound as well, as shown in Notebook-code (which corresponds to Figure 4 in the academic paper), demonstrates its robustness and theoretical consistency.

# Create specific grid for Figure 4 with max point at 3.0
m_grid_fig4 = np.linspace(IndShockTruthSol.mNrmMin + 0.01, 3.0, 100)

# Evaluate consumption functions for comparison at Figure 4 grid points
c_mom_fig4 = IndShockMoMApproxSol.cFunc(m_grid_fig4)  # MoM consumption
c_opt_fig4 = TruthOpt.cFunc(m_grid_fig4)  # Optimist consumption
c_pes_fig4 = TruthPes.cFunc(m_grid_fig4)  # Pessimist consumption
c_tight_fig4 = TruthTight.cFunc(m_grid_fig4)  # Tight upper bound

# Figure 4: MoM Consumption Function
plot_consumption_bounds(
    m_grid=m_grid_fig4,
    c_main=c_mom_fig4,
    c_opt=c_opt_fig4,
    c_pes=c_pes_fig4,
    title="Figure 4: MoM Consumption Function",
    subtitle="MoM Consumption Respects Theoretical Bounds",
    legend="MoM Approximation",
    c_tight=c_tight_fig4,  # Automatically shown since c_tight is provided
    solution=IndShockMoMApproxSol,
)

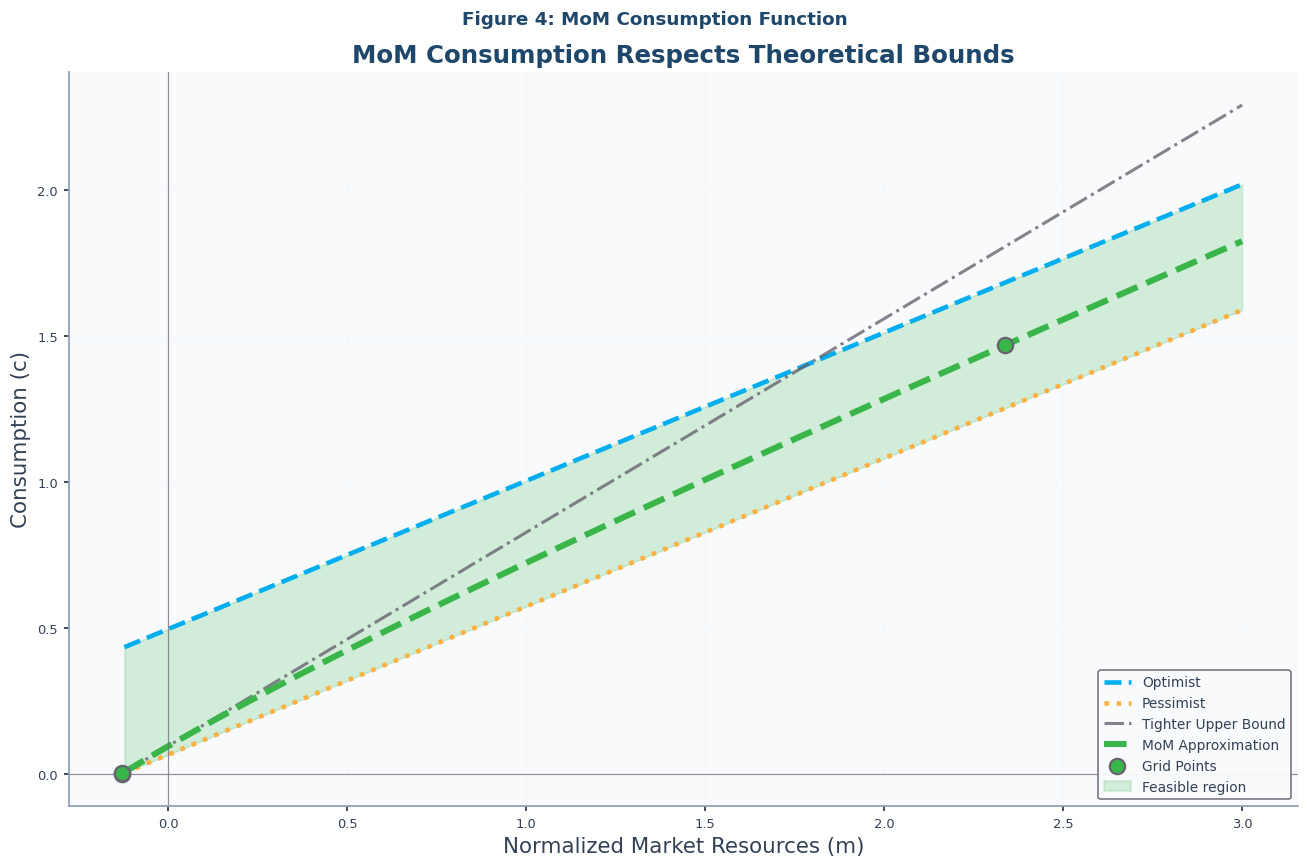
Bound Preservation: MoM consumption stays within theoretical bounds and below tight bound.

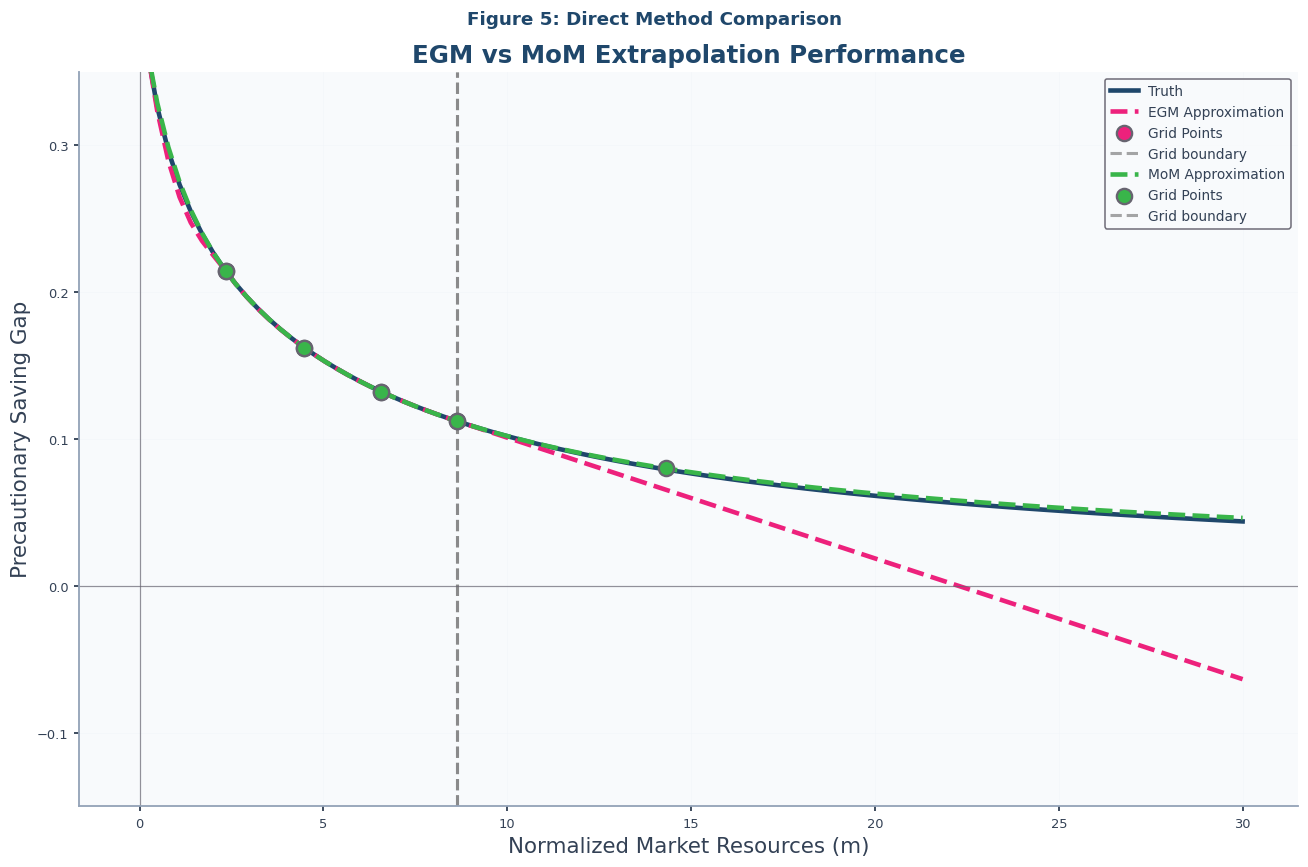
Figure 5: Direct Method Comparison¶

We now arrive at the decisive comparison between the Endogenous Grid Method and the Method of Moderation. This figure plots the precautionary saving gaps from both the EGM and MoM solutions on the same axes, alongside the high-precision “truth” solution.

All three solutions are generated from the same underlying economic parameters, and both the EGM and MoM approximations use the same 5-point sparse grid. The difference in their extrapolation behavior is therefore entirely attributable to the solution method itself. The results, presented in Notebook-code, clearly show the superiority of the Method of Moderation for problems where extrapolation is a concern.

# Use the same wide grid for consistent comparison
m_grid_comparison = m_grid_wide

# Combined comparison: Truth, EGM failure, and MoM success
plot_precautionary_gaps(
    m_grid=m_grid_comparison,
    truth_gap=truth_gap(m_grid_comparison),
    approx_gap=[egm_approx_gap(m_grid_comparison), mom_approx_gap(m_grid_comparison)],
    legend=["EGM Approximation", "MoM Approximation"],
    title="Figure 5: Direct Method Comparison",
    subtitle="EGM vs MoM Extrapolation Performance",
    solution=IndShockMoMApproxSol,  # Use MoM solution for grid points
    grid_points=True,
)

Method of Moderation Framework¶

Figure 6: Moderation Ratio Function $\modRte(\mNrm)$ ¶

Definition: The Moderation Ratio

The central element of the Method of Moderation is the moderation ratio, $\modRte(\mNrm)$ , which precisely quantifies the realist consumer’s behavior relative to the theoretical bounds. As defined in equation (12) of the paper, it is:

\modRte(\mNrm) = \frac{\cFuncOpt(\mNrm) - \cFuncReal(\mNrm)}{\cFuncOpt(\mNrm) - \cFuncPes(\mNrm)}

(1)

This ratio is guaranteed to be strictly between 0 and 1 for all valid levels of market resources, a property that follows from the consumer’s prudence (i.e., a convex marginal utility function) and the presence of bounded income shocks Carroll & Kimball, 1996. It has the following interpretation:

$\modRte = 0$ : The realist behaves like the optimist (at high levels of wealth).
$\modRte = 1$ : The realist behaves like the pessimist (at low levels of wealth).
$0 < \modRte < 1$ : The realist engages in a balanced moderation, reflecting partial prudence.

This figure plots the moderation ratio as a function of market resources, revealing the consumer’s risk management strategy across the wealth distribution, as shown in Notebook-code.

# Create grid mirroring paper's wide evaluation range
m_grid_fig5 = np.linspace(IndShockMoMApproxSol.mNrmMin + 0.01, 50, 200)

# Access the moderation functions from the MoM solution
transformed_func = IndShockMoMApproxSol.cFunc  # TransformedFunctionMoM
modRteFunc = transformed_func.modRteFunc  # $\modRte(\logmNrmEx)$ function
logitModRteFunc = transformed_func.logitModRteFunc  # transformation function

# Convert market resources to $\logmNrmEx$ ("mu" in the paper: $\logmNrmEx = \log(\mNrm-\mNrmMin)$)
from moderation import expit_moderate, log_mnrm_ex

m_min = transformed_func.mNrmMin
mu_grid_fig5 = log_mnrm_ex(m_grid_fig5, m_min)

# Evaluate moderation ratio $\modRte(\logmNrmEx)$ via transformation and inverse
chi_values_fig5 = logitModRteFunc(mu_grid_fig5)
omega_values_fig5 = expit_moderate(chi_values_fig5)

# Figure 6: Moderation Ratio Function (paper Fig. 6 counterpart)
plot_moderation_ratio(
    m_grid=m_grid_fig5,
    omega_values=omega_values_fig5,
    title=r"Figure 6: Consumption Moderation Ratio $\omega(m)$",
    subtitle="Wealth-Dependent Moderation Between Bounds",
    solution=IndShockMoMApproxSol,
    grid_type="consumption",
)

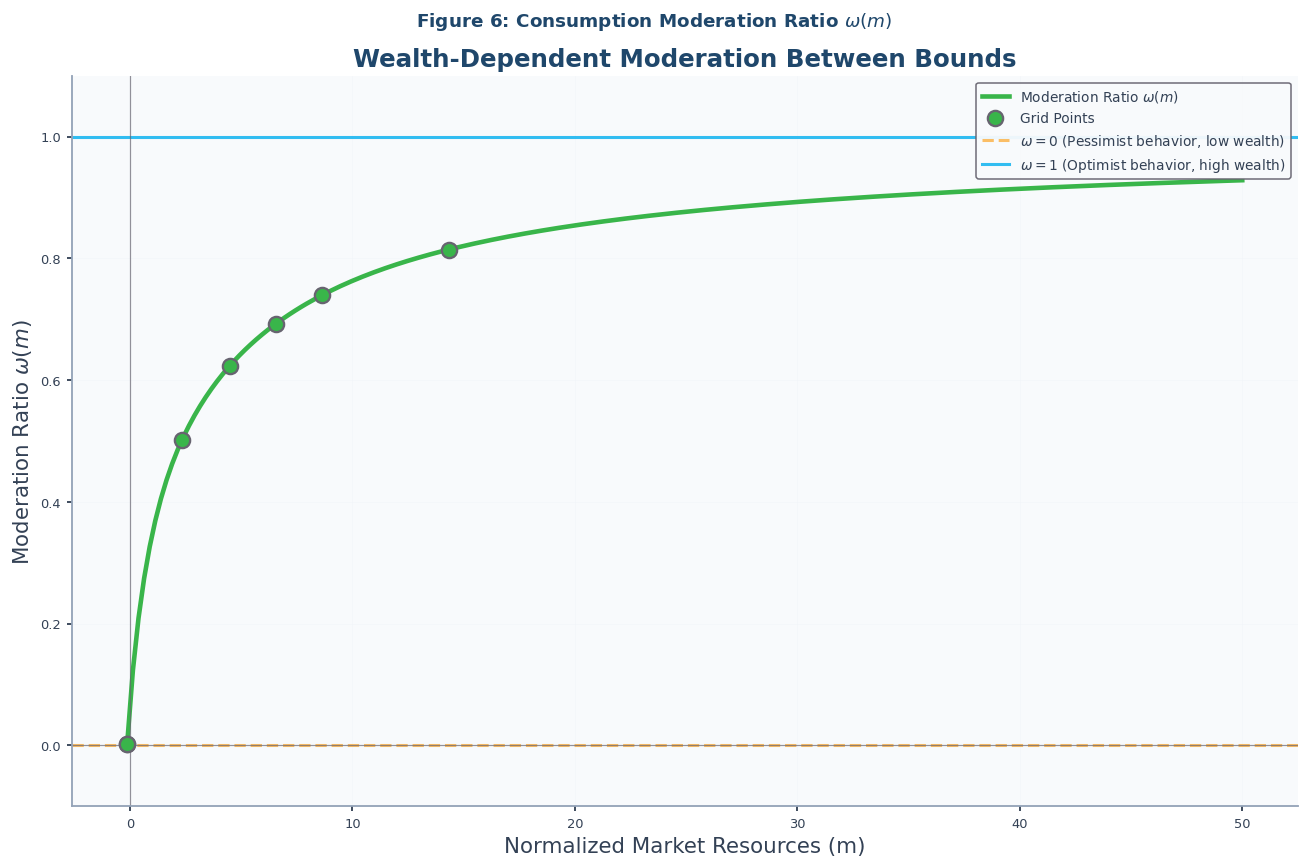
Figure 7: The Logit Transformation¶

Definition: The Logit Transformation

While the moderation ratio, $\modRte(\mNrm)$ , is economically intuitive, it is not ideal for numerical interpolation because it is bounded between 0 and 1. To address this, the Method of Moderation employs a logit transformation, which maps the bounded moderation ratio into an unbounded space. As defined in equation (13) of the paper, the transformed variable, $\logitModRte(\logmNrmEx)$ , is:

\logitModRte(\logmNrmEx) = \log\left(\frac{1 - \modRte(\logmNrmEx)}{\modRte(\logmNrmEx)}\right)

(2)

where $\logmNrmEx = \log(\mNrm - \mNrmMin)$ is the log of “excess” market resources. This transformation is the key to MoM’s numerical stability and superior extrapolation properties. As Notebook-code will show, the $\logitModRte$ function is nearly linear, which makes it exceptionally well-suited for interpolation.

# Create market resources grid from near constraint to high wealth to show full behavior
m_grid_wide = np.linspace(m_min + 0.001, 50, 200)

# Convert to mu grid for x-axis (this is the natural domain for logit function)
mu_grid_chi = log_mnrm_ex(m_grid_wide, m_min)

# Evaluate logit function over this extended range
chi_values_fig6 = logitModRteFunc(mu_grid_chi)

# Figure 7: Logit Transformation Function plotted over mu (log excess resources)
# X-axis will be mu = log(m - mNrmMin), Y-axis will be logit(omega)
plot_logit_function(
    mu_grid=mu_grid_chi,  # mu values for x-axis (log excess market resources)
    chi_values=chi_values_fig6,
    title="Figure 7: Logit Transformation for Stable Extrapolation",
    subtitle="Unbounded Transformation for Stable Extrapolation",
    solution=IndShockMoMApproxSol,
    grid_points=True,
)

Mathematical Properties of

\logitModRte(\logmNrmEx)

The logit transformation exhibits several key properties visible in the figure (with $\logitModRteMu>0$ ):

Unbounded domain: $\logitModRte \in (-\infty, \infty)$ allows smooth interpolation without artificial constraints
Monotonically decreasing: Higher wealth (larger $\logmNrmEx$ ) corresponds to lower $\logitModRte$ values (closer to optimist behavior)
Asymptotic linearity with positive slope: $\logitModRteMu>0$ as $\logmNrmEx \to \infty$ , ensuring stable extrapolation
Economic interpretation:
- $\logitModRte > 0$ : Realist closer to optimist (low precautionary saving)
- $\logitModRte < 0$ : Realist closer to pessimist (high precautionary saving)
- $\logitModRte \approx 0$ : Balanced between extremes

This mathematical elegance translates directly into superior numerical properties for consumption function approximation.

Function Properties and Bounds¶

Figure 8: MoM MPC Bounded by Theory¶

Beyond the consumption function itself, its derivative—the marginal propensity to consume (MPC)—is of central economic importance. The MPC, $\partial c / \partial m$ , measures the change in consumption for a one-unit change in market resources and is a key input for macroeconomic models and policy analysis. It is crucial for understanding:

Monetary policy transmission: How interest rate changes affect spending
Fiscal policy effectiveness: How tax rebates stimulate consumption
Wealth effects: How asset price changes impact the economy

Just as with the consumption function, the MPC must respect theoretical bounds. As detailed in the paper's extensions, the MPC is bounded by a minimum value, $\MPCmin$ (the MPC of the risk-free optimist), and a maximum value, $\MPCmax$ (the MPC as resources approach the borrowing constraint). These bounds are fundamental properties of consumption models with prudence Carroll, 2001. This figure demonstrates that the MPC derived from the MoM consumption function correctly lies within these theoretical bounds, as shown in Notebook-code.

# Calculate MPCs - now using the implemented MoM MPC derivative
m_grid_mpc = np.linspace(IndShockTruthSol.mNrmMin + 0.01, 10, 100)
mpc_mom = IndShockMoMApproxSol.cFunc.derivative(m_grid_mpc)  # MoM MPC (varies with wealth)
mpc_opt_const = IndShockTruthSol.MPCmin  # Optimist MPC (constant)
mpc_tight_const = IndShockTruthSol.MPCmax  # Tight bound MPC (constant)

# Create constant arrays for plotting
mpc_opt_vals = np.full_like(m_grid_mpc, mpc_opt_const)
mpc_tight_vals = np.full_like(m_grid_mpc, mpc_tight_const)

# Figure 8: MoM MPC Bounds
plot_mom_mpc(
    m_grid=m_grid_mpc,
    mpc_values=mpc_mom,
    mpc_opt_vals=mpc_opt_vals,
    mpc_tight_vals=mpc_tight_vals,
    title="Figure 8: MoM MPC Bounded by Theory",
    subtitle="MoM MPC Stays Within Theoretical Bounds",
    mpc_label="MoM MPC",
    solution=IndShockMoMApproxSol,
    grid_points=True,  # Explicitly enable grid points
)

MPC Economic Interpretation

MPC Bounds Respected: The MoM marginal propensity to consume declines with $\mNrm$ as theory predicts, staying between $\MPCmin$ and $\MPCmax$ . This reflects fundamental economic principles:

Poor consumers spend windfalls immediately (high $\MPC$ , approaching $\MPCmax$ )
Rich consumers save most windfalls (low $\MPC$ , approaching $\MPCmin$ )
This reflects diminishing marginal utility of consumption
$\MPC$ decline shows wealth effects diminish with higher market resources
Linear consumption functions have constant $\MPC$ reflecting perfect-foresight assumptions

The bounds ensure that $\MPC$ values remain economically sensible, with the realist $\MPC$ lying between the tight upper bound $\MPCmax$ and optimist lower bound $\MPCmin$ .

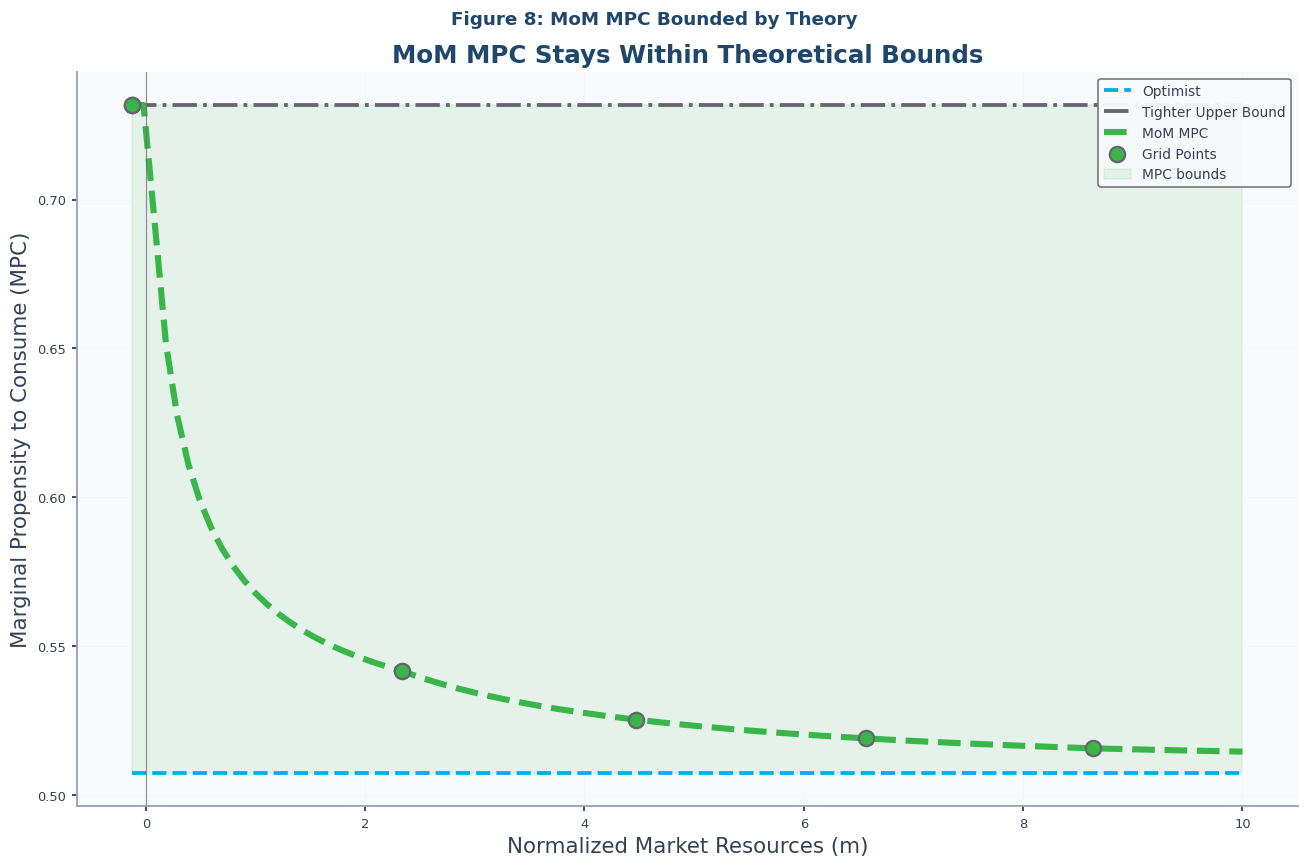
Figure 9: Value Functions Bounded by Theory¶

We now turn from the policy function, $c(m)$ , to the value function, $v(m)$ , which represents the consumer’s expected lifetime utility as a function of current market resources. The value function is a cornerstone of dynamic programming and provides a comprehensive measure of a consumer’s well-being.

This figure serves two purposes. First, it demonstrates that the value function, like the consumption function, is bounded by the optimist and pessimist solutions Aiyagari, 1994Huggett, 1993. Second, it compares the value functions generated by the high-precision “truth” model, the sparse-grid EGM, and the sparse-grid MoM. This allows us to see how accurately each method approximates the true value function, as shown in Notebook-code.

# Create wealth grid specifically for value functions (starting from mNrmMin + 0.001)
m_grid_vfunc = np.linspace(IndShockEGMApproxSol.mNrmMin + 0.001, 3.0, 100)

# Evaluate value functions on the grid
v_truth = IndShockTruthSol.vFunc(m_grid_vfunc)  # Truth
v_opt = TruthOpt.vFunc(m_grid_vfunc)  # Optimist
v_pes = TruthPes.vFunc(m_grid_vfunc)  # Pessimist
v_tight = TruthTight.vFunc(m_grid_vfunc)  # Tight upper bound
v_egm_sparse = IndShockEGMApproxSol.vFunc(
    m_grid_vfunc,
)  # EGM Approximation
v_mom_sparse = IndShockMoMApproxSol.vFunc(m_grid_vfunc)  # MoM Approximation

# Figure 9: Value Functions (truth, optimist, pessimist, tight, EGM, MoM)
plot_value_functions(
    m_grid=m_grid_vfunc,
    title="Figure 9: Value Functions Bounded by Economic Theory",
    subtitle="Value Function: True Solution vs Sparse Approximations",
    v_truth=v_truth,
    v_opt=v_opt,
    v_pes=v_pes,
    v_tight=v_tight,
    v_egm_sparse=v_egm_sparse,
    v_mom_sparse=v_mom_sparse,
    figure_num=7,
    mom_solution=IndShockMoMApproxSol,
    egm_solution=None,
)

Value Function Economic Interpretation

This figure shows the theoretical bounds, sparse approximations, and truth solution:

Truth (blue) - realist solution with uncertainty
Optimist (light blue) - highest possible utility
Pessimist (yellow) - lowest possible utility
Tighter Upper Bound (orange) - refined upper bound using maximum MPC
EGM Approximation (pink) - sparse grid approximation
MoM Approximation (green) - Method of Moderation approximation with visible grid points

Both EGM and MoM approximations use the same 5 sparse grid points, but MoM provides superior approximation quality, staying closer to the truth solution while respecting all theoretical bounds. The grid points (shown only for MoM to avoid duplication) reveal exactly where the sparse interpolation nodes are located, demonstrating the efficiency of the Method of Moderation approach.

The gap between optimist and pessimist values represents the cost of uncertainty - how much lifetime utility is reduced when facing income uncertainty rather than perfect foresight.

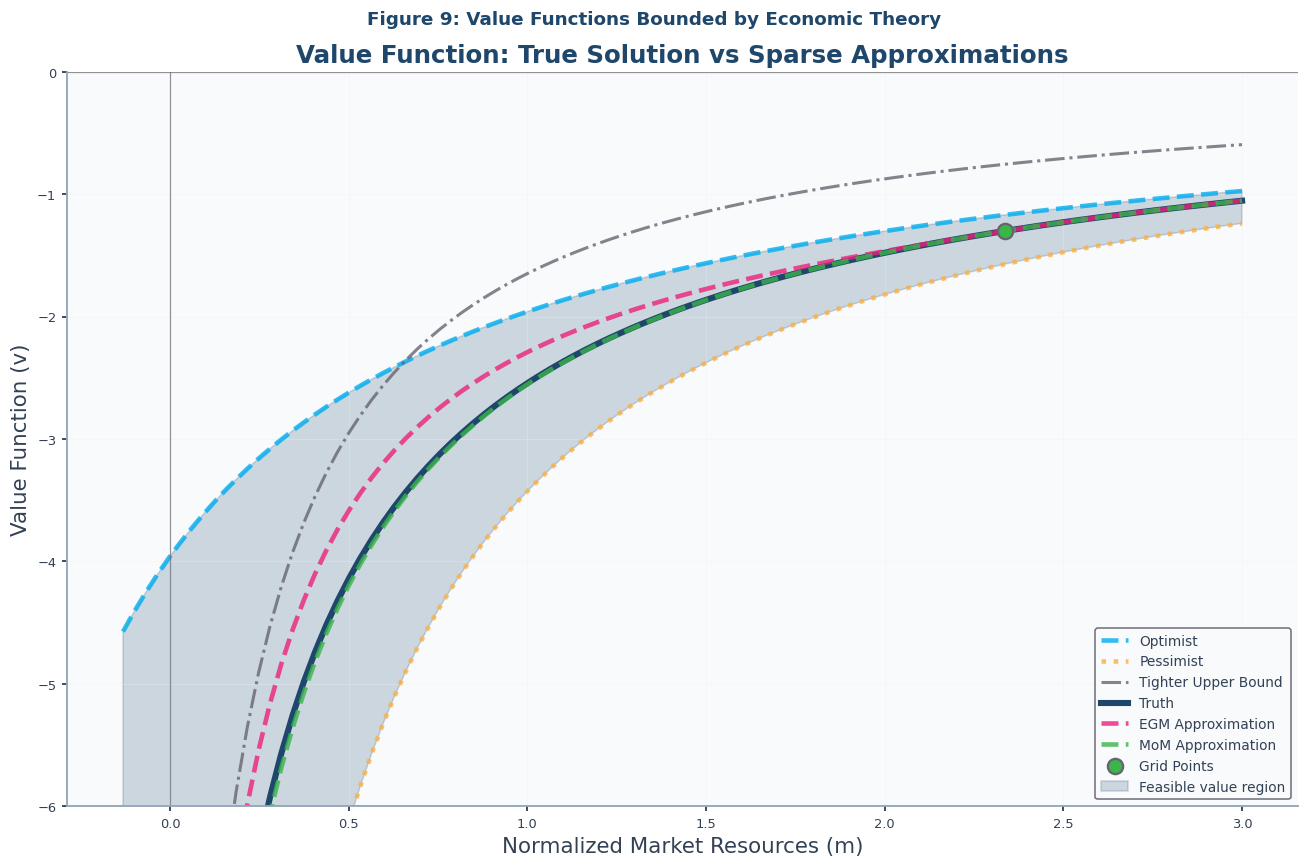
Figure 10: Inverse Value Functions $\vInv(\mNrm)$ ¶

For numerical stability and easier interpretation, it is often convenient to work with the inverse value function, $\vInv(\mNrm) = \uFunc^{-1}(\vFunc(\mNrm))$ . This function represents the constant level of consumption that would yield the same lifetime utility as the value function at a given level of market resources. It can be thought of as the “consumption equivalent” of lifetime utility.

This transformation is particularly useful because, as this figure shows, it tends to be much more linear than the value function itself, especially near the borrowing constraint. This makes it better suited for numerical interpolation and is a key reason for its use in HARK. This figure compares the inverse value functions from our three solutions, again demonstrating the accuracy of the MoM approximation, as shown in Notebook-code.

# Evaluate inverse value functions on the same grid as Figure 8
vNvrs_truth = IndShockTruthSol.vFunc.vFuncNvrs(m_grid_vfunc)  # Truth inverse value
vNvrs_opt = TruthOpt.vFunc.vFuncNvrs(m_grid_vfunc)  # Optimist inverse value
vNvrs_pes = TruthPes.vFunc.vFuncNvrs(m_grid_vfunc)  # Pessimist inverse value
vNvrs_egm_sparse = IndShockEGMApproxSol.vFunc.vFuncNvrs(
    m_grid_vfunc,
)  # EGM inverse value
vNvrs_mom_sparse = IndShockMoMApproxSol.vFunc.vFuncNvrs(
    m_grid_vfunc,
)  # MoM inverse value

# Figure 10: Inverse Value Functions
plot_value_functions(
    m_grid=m_grid_vfunc,
    title="Figure 10: Inverse Value Functions",
    subtitle="Inverse Value Function: Consumption-Equivalent Utility",
    v_truth=vNvrs_truth,
    v_opt=vNvrs_opt,
    v_pes=vNvrs_pes,
    v_tight=None,
    v_egm_sparse=vNvrs_egm_sparse,
    v_mom_sparse=vNvrs_mom_sparse,
    figure_num=8,
    mom_solution=IndShockMoMApproxSol,
    egm_solution=IndShockEGMApproxSol,
)

Inverse Value Function Economic Interpretation

The inverse value functions provide an intuitive consumption-equivalent interpretation of lifetime utility:

Truth (blue) - consumption equivalent of realist lifetime utility
Optimist (light blue) - consumption equivalent with no uncertainty
Pessimist (yellow) - consumption equivalent with worst-case scenarios
EGM Approximation (pink) - sparse grid approximation
MoM Approximation (green) - Method of Moderation approximation

The inverse transformation $\vInv(\mNrm) = \uFunc^{-1}(\vFunc(\mNrm))$ converts utility units into consumption units, making the economic interpretation more intuitive. For example, if $\vInv(5) = 0.8$ , then having 5 units of wealth provides the same lifetime utility as consuming 0.8 units forever.

The ordering and gaps between inverse value functions mirror those in Figure 8, but the inverse transformation linearizes the problem near the borrowing constraint, which is why HARK uses this representation for numerical interpolation.

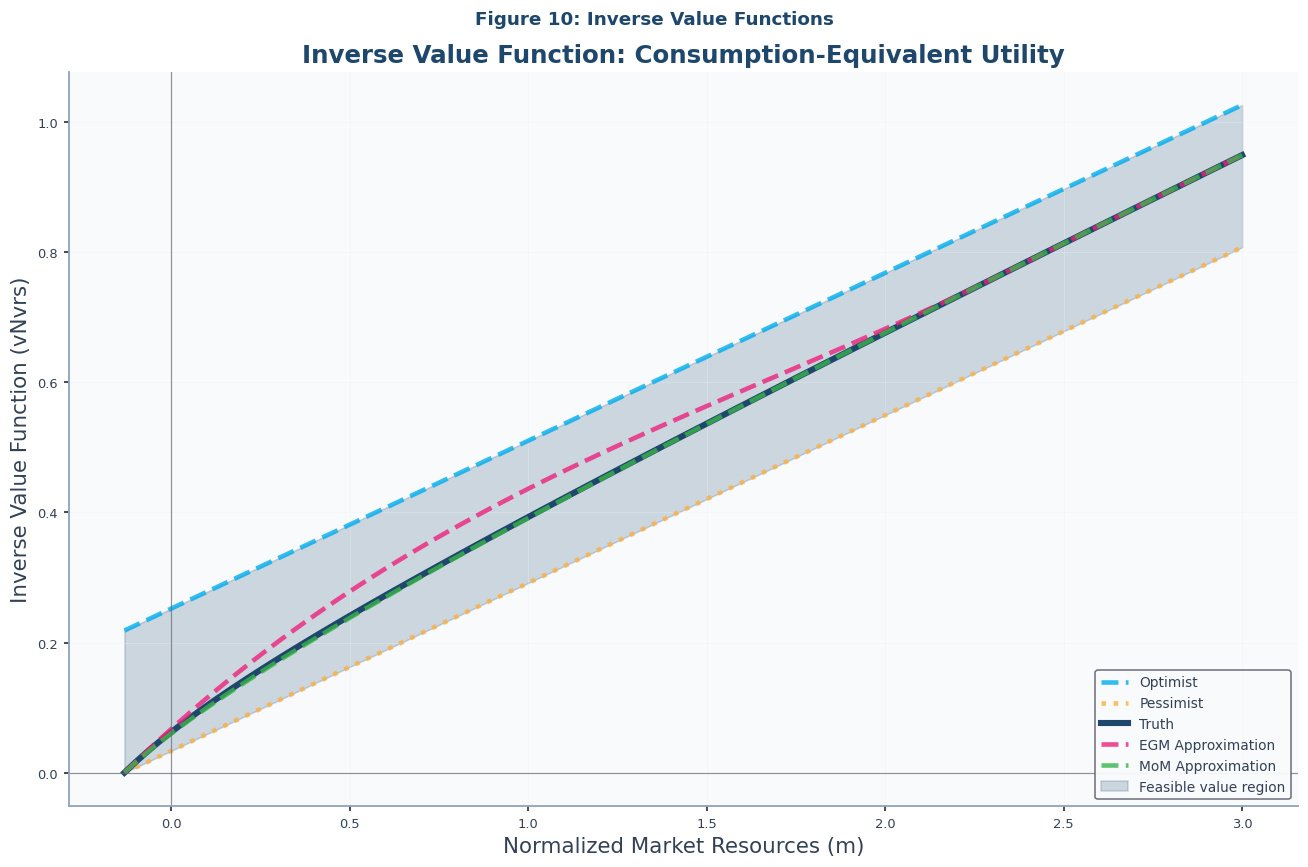
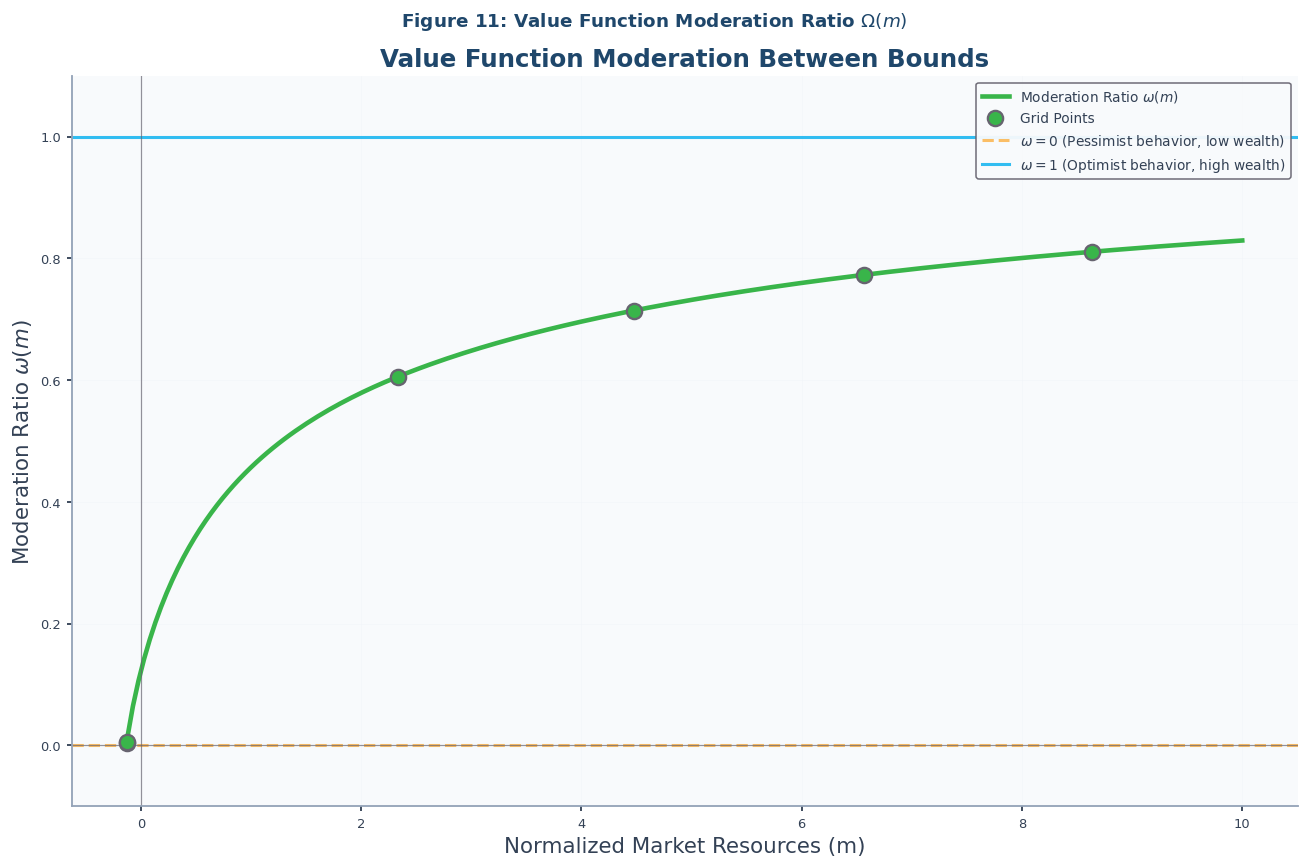
Figure 11: Value Function Moderation Ratio¶

The final figure demonstrates the versatility of the Method of Moderation. Because the method is built on the general principle of moderating between theoretical bounds, it can be applied not just to the consumption function, but to any function that is similarly bounded. Here, we apply it to the inverse value function.

The moderation ratio for the inverse value function is defined analogously to the consumption moderation ratio:

\valModRte(\mNrm) = \frac{\vInvOpt(\mNrm) - \vInvReal(\mNrm)}{\vInvOpt(\mNrm) - \vInvPes(\mNrm)}

(3)

This ratio measures how the welfare cost of uncertainty (the gap between the optimist and realist inverse value functions) changes with the level of market resources. As the figure shows, the pattern is similar to that of the consumption moderation ratio, providing further evidence of the robustness of the Method of Moderation, as shown in Notebook-code.

# Access the value function moderation functions from the MoM solution
# Extract value function moderation functions
vfunc_transformed = (
    IndShockMoMApproxSol.vFunc.vFuncNvrs
)  # TransformedFunctionMoM for value function
vfunc_modRteFunc = (
    vfunc_transformed.modRteFunc
)  # $\valModRte(\logmNrmEx)$ function for value function
vfunc_logitModRteFunc = (
    vfunc_transformed.logitModRteFunc
)  # $\logitValModRte(\logmNrmEx)$ function for value function

# Create specific grid for Figure 10 with xlim at 10
m_grid_vfunc_mod = np.linspace(IndShockMoMApproxSol.mNrmMin + 0.01, 10, 200)

# Convert to $\logmNrmEx$ for evaluation
mu_grid_vfunc = log_mnrm_ex(m_grid_vfunc_mod, m_min)

# Evaluate value function moderation ratio $\valModRte(\logmNrmEx)$ by using chi function and inverse transformation
vfunc_chi_values = vfunc_logitModRteFunc(mu_grid_vfunc)
vfunc_omega_values = expit_moderate(vfunc_chi_values)

# Figure 11: Value Function Moderation Ratio
plot_moderation_ratio(
    m_grid=m_grid_vfunc_mod,
    omega_values=vfunc_omega_values,
    title=r"Figure 11: Value Function Moderation Ratio $\Omega(m)$",
    subtitle="Value Function Moderation Between Bounds",
    solution=IndShockMoMApproxSol,
    grid_type="value",
)

Further Extensions: Stochastic Rate of Return¶

The analysis so far has assumed a constant, risk-free interest rate. The Method of Moderation can be extended to incorporate a stochastic rate of return on assets. In the case where the rate of return is independently and identically distributed (i.i.d.), the classic work of Samuelson (1969) and Merton (1969)Merton (1971) shows that the consumption function remains linear for a consumer with no labor income, with a constant MPC that depends on the distribution of returns.

This result allows the MoM framework to be applied directly, simply by substituting the stochastic-return MPC for the perfect-foresight MPC in the definition of the optimist’s consumption function. As wealth becomes very large, the consumption function becomes asymptotically linear as the precautionary motive related to labor income vanishes Benhabib et al., 2018. For a detailed derivation, see Carroll (2020). The more complex case of serially correlated returns is a topic for future research.

Summary: Why the Method of Moderation Matters¶

This notebook has demonstrated the Method of Moderation from both a practical and a theoretical perspective. We began by showing that the standard Endogenous Grid Method, while computationally efficient, can produce economically nonsensical results when extrapolating from a sparse grid. We then introduced the theoretical underpinnings of MoM, which is built on the insight that the true consumption function is always bounded by analytical optimist and pessimist solutions.

The core innovation of the Method of Moderation is to solve the model in a transformed space defined by these bounds. By interpolating a moderation ratio via an asymptotically linear logit transformation, MoM ensures that its solutions respect theoretical constraints by construction. This approach not only solves the extrapolation problem but also provides a robust and efficient method for solving consumption-saving models.

Key Advantages:

Theoretical Consistency: Solutions always respect economic bounds, preventing issues like negative precautionary saving.
Numerical Stability: The use of transformations and analytical bounds leads to robust and accurate solutions.
Computational Efficiency: MoM builds upon the speed of EGM, adding only a small computational overhead.

These features make the Method of Moderation a powerful tool for a wide range of applications, from academic research to policy analysis in central banks and other institutions.

For complete theoretical development see The Method of Moderation.

References¶

Friedman, M. (1957). A Theory of the Consumption Function. Princeton University Press.
Muth, J. F. (1960). Optimal Properties of Exponentially Weighted Forecasts. Journal of the American Statistical Association, 55(290), 299–306.
Carroll, C. D. (2020). Solving microeconomic dynamic stochastic optimization problems [Techreport]. Johns Hopkins University. https://www.econ2.jhu.edu/people/ccarroll/SolvingMicroDSOPs.pdf
Leland, H. E. (1968). Saving and Uncertainty: The Precautionary Demand for Saving. Quarterly Journal of Economics, 82(3), 465–473. 10.2307/1879518
Sandmo, A. (1970). The Effect of Uncertainty on Saving Decisions. Review of Economic Studies, 37(3), 353–360. 10.2307/2296725
Kimball, M. S. (1990). Precautionary Saving in the Small and in the Large. Econometrica, 58(1), 53–73. 10.3386/w2848
Carroll, C. D. (1997). Buffer-Stock Saving and the Life Cycle/Permanent Income Hypothesis. Quarterly Journal of Economics, 112(1), 1–55. 10.1162/003355397555109
Stachurski, J., & Toda, A. A. (2019). An Impossibility Theorem for Wealth in Heterogeneous-Agent Models. Journal of Economic Theory.
Ma, Q., Stachurski, J., & Toda, A. A. (2020). The Income Fluctuation Problem and the Evolution of Wealth. Journal of Economic Theory, 187, 105003. 10.1016/j.jet.2020.105003
Carroll, C. D. (2006). The method of endogenous gridpoints for solving dynamic stochastic optimization problems. Economics Letters, 91(3), 312–320.
Barillas, F., & Fernández-Villaverde, J. (2007). A Generalization of the Endogenous Grid Method. Journal of Economic Dynamics and Control, 31(8), 2698–2712.
Hintermaier, T., & Koeniger, W. (2010). The Method of Endogenous Gridpoints with Occasionally Binding Constraints among Endogenous Variables. Journal of Economic Dynamics and Control, 34(10), 2074–2088. 10.1016/j.jedc.2010.05.002
Fella, G. (2014). A Generalized Endogenous Grid Method for Non-smooth and Non-concave Problems. Review of Economic Dynamics, 17(2), 329–344. 10.1016/j.red.2013.07.001
Iskhakov, F., Jørgensen, T. H., Rust, J., & Schjerning, B. (2017). The Endogenous Grid Method for Discrete–Continuous Dynamic Choice Models with (or without) Taste Shocks. Quantitative Economics, 8(2), 317–365. 10.3982/qe643
White, M. N. (2015). The Method of Endogenous Gridpoints in Theory and Practice. Journal of Economic Dynamics and Control, 60, 26–41. 10.1016/j.jedc.2015.08.001

The Method of Moderation: Illustrative Notebook

Model Foundations: The Friedman-Muth Income Process¶

The Extrapolation Problem in Consumption-Saving Models¶

Consumption Function Analysis¶

Figure 1: The EGM Extrapolation Problem¶

Figure 2: Truth Bounded by Theory¶

Figure 3: Method of Moderation Solution¶

Figure 4: MoM Consumption Function¶

Figure 5: Direct Method Comparison¶

Method of Moderation Framework¶

Figure 6: Moderation Ratio Function ωˉ(m)\modRte(\mNrm)ωˉ(m)¶

Figure 7: The Logit Transformation¶

Function Properties and Bounds¶

Figure 8: MoM MPC Bounded by Theory¶

Figure 9: Value Functions Bounded by Theory¶

Figure 10: Inverse Value Functions Λ(m)\vInv(\mNrm)Λ(m)¶

Figure 11: Value Function Moderation Ratio¶

Further Extensions: Stochastic Rate of Return¶

Summary: Why the Method of Moderation Matters¶

Figure 6: Moderation Ratio Function $\modRte(\mNrm)$ ¶

Figure 10: Inverse Value Functions $\vInv(\mNrm)$ ¶